Recommender Systems Part 3: Candidate Generation - Collaborative Filtering (continued)
- Jul 28, 2023
- 4 min read
Binary Labels: Favorites, Likes, and Clicks
Many important applications of recommender systems or collaborative filtering algorithms involve binary labels, where instead of a user giving a 0-5 stars rating, they give you a like or don't like. Let's take a look at how to generalize the algorithm we looked at in yesterday's post to this setting.
Here's an example of collaborative filtering data set with binary labels:

By predicting how likely Alice, Bob, Carol, and Dave are to like the items they have not yet rated, we can then decide how much we should recommend these items to them. There are many ways of defining the labels 1, 0, or ?, some examples include:
did user j purchase an item after being shown?
did user j favorite or like an item?
did user j spend at least 30 seconds with an item?
did user j click on an item?
Meaning of ratings for our example:
1: engaged after being shown item
0: did not engage after being shown item
?: item not shown yet
previously, we predict y(i,j) with the following prediction function:
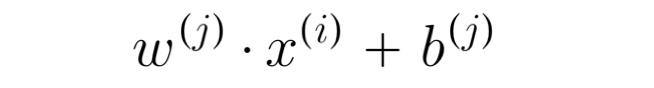
For binary labels, we will use this function instead:

Loss function for binary labels, for one user example:

Cost function for all examples:

where f(x) is:

Recommender Systems Implementation
Mean Normalization
When building a recommender system with numbers, such as movie ratings from 0-5 stars, your algorithm will run more efficiently and perform better if you first carry out mean normalization. That is, if you normalize the movie ratings to have consistent average value.
Let's look at an example from the movie data we have used, and add a new user 5, Eve, who has not yet rated any movie. Adding mean normalization will help the algorithm make better prediction on the user Eve. With the previous algorithm, it will predict that if you have a new user that has not yet rated anything, it will rate all movies 0 stars and that wouldn't be helpful.
To describe mean normalization, take all of the values including all the '?' and put them in a 2-D matrix and compute the average rating that was given:

image taken from Deeplearning.ai Machine learning specialization by Andrew Ng
As we can see in the image above, we will take subtract each rating from the original ratings with the mean, and we'll get the result shown on the right side of the image, which will be our new y(i,j)
With this, we can learn our parameters w,x,b like we previously did, but because we have subtracted mean from each rating, we will have to add it back after the computation.
The effect of this algorithm for the new user Eve is, the initial guesses would be equal to the mean of all user for these movies.
In this example, we normalized by row, and it is also possible to normalize by column.
TensorFlow implementation of Collaborative Filtering
We're going to use a very simplified cost function for this example:

the gradient descent algorithm we will be using in this example, we will fix b = 0 for this example:

w = tf.Variable(3.0) # parameters we want to optimize
x = 1.0
y = 1.0 # target value
alpha = 0.01
iterations = 30
for iter in range(iterations):
# use TensorFlow's gradient tape to record steps used to compute
# the cost J, to enable auto differentiation (auto diff)
with tf.GradientTape() as tape:
fwb = w*x
costJ = (fwb - y) ** 2
# use the gradient tape to calculate the gradients of the cost
# wrt the parameter w
[dJdw] = tape.gradient(costJ, [w])
# run one step of gradient descent by updating the value of w to
# reduce the cost
w.assign_add(-alpha * dJdw) # tf.Variable require special function to modifyOnce we found our parameters with gradient descent, this is how we can implement collaborative filtering with TensorFlow:
def cofi_cost_func_v(X, W, b, Y, R, lambda_):
j = (tf.linalg.matmul(X, tf.transpose(W)) + b - Y) * R
J = 0.5 * tf.reduce_sum(j**2) + (lambda_/2) * (tf.reduce_sum(X**2) + tf.reduce_sum(W**2))
return J# instantiate an optimizer
optimizer = keras.optimizers.Adam(learning_rate=1e-1)
iterations = 200
for iter in range(iterations):
# use TensorFlow's gradient tape to record the operations used to
# compute the cost
with tf.GradientTape() as tape:
# compute the cost (forward pass is included in cost)
cost_value = cofi_cost_func_v(X, W, b, Ynorm, R, num_users, num_movies, lambda)
# use the gradient tape to automatically retrieve the gradients
# of the trainable variables wrt the loss
grads = tape.gradient(cost_value, [X, W, b])
# run one step of gradient descent by updating the value of the
# variables to minimize the loss
optimizer.apply_gradients(zip(grads, [X, W, b]))Notations:
Ynorm = mean normalized
R = which values have rating
zip() = a function in python that re-arranges the numbers into appropriate ordering for the applied gradient function
Finding related item
The collaborative filtering algorithm we have seen gives us a great way to find related items. As part of the collaborative filtering we have discussed, we learned features x(i) for every item i (movie i, or other items you're recommending)
In practice, when you use this algorithm to learn the features x(i), looking at the individual features, it will be difficult to interpret, but nonetheless, collectively, they convey something about what the movie is like.
So, let's say, you would like to find other movies or items related to i:
find item k with x(k) similar to x(i):

This function would be the distance between x(k) and x(i), this squared distance can also be written as:

If you find not just one movie with the smallest distance between x(k) and x(i), but 5-10 items with the most similar feature vectors, then you end up finding 5-10 related items to the item x(i)
Limitations of collaborative filtering:
cold start problem: how to rank new items that few users have rated? show something to new users who have rated only a few items?
doesn't give you a natural way to use additional information about items or users such as: genres, movie-stars, demographics, etc.
To calculate mean normalization to do feature scaling of the ratings, you can use the following function:






Comments