Day 10: Summary of Regression with Multiple Variables
- Jul 4, 2023
- 2 min read

Vectorization
When implementing a learning algorithm, using vectorization will both make our code shorter and make it run much more efficiently.
With vectorization, we can easily implement functions with many input features, which we can implement with NumPy's dot function:
f = np.dot(w, x) + bThe NumPy dot function is a vectorized implementation of the dot product operation between 2 vectors.
the reason that vectorization implementation is much faster is because it is able to use parallel hardware in your computer, and in a single step, it performs distinct functions all at the same time in parallel
Feature Scaling
Feature scaling is a technique to scale data that will better the performance of a Machine Learning Model
There are 3 different way to scale features:
divide by max
mean normalization
z-score normalization
divide by max
Features in this method is done by dividing each feature by the maximum value in the list of features.
for example, if we're looking x features:
x1 = 300
max(x) = 2000
x1-rescaled = 300/2000 = 0.15
mean normalization
In mean normalization, you start with the original features, and then, you re-scale them so that both of them are centered around zero, where they previously only had values greater than zero, they now have values ranging from -1 to 1
The formula for mean normalization:
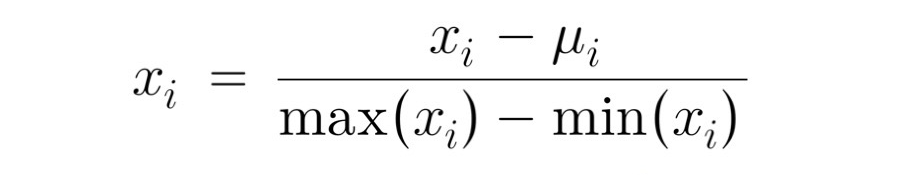
z-score normalization
To implement z-score normalization, you will need to calculate standard-deviation(σ) of each feature.
The formula for z-score normalization:

z-score normalization implementation
z-score with numpy:
import numpy as np
def z_score_normalize_features(X):
# find the mean of each column or feature
mu = np.mean(X, axis=0)
# find the standard-deviation of each column or feature
sigma = np.std(X, axis=0)
# element-wise, subtract mu for that column from each example, divide by std for that column
X_norm = (X - mu) / sigma
return X_norm, mu, sigmaz-score with Scikit-Learn:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_norm = scaler.fit_transform(X_train)Feature Engineering
Feature Engineering: using intuition to design new features, by transforming and/or combining original features
The choice of features can have a huge impact on your learning algorithm's performance. Depending on what insights you may have into the application, rather than just taking the features that you happen to have started off with, sometimes by defining new features, you may be able to get a better model.
Polynomial Regression
By taking the ideas of multiple linear regression and feature engineering, we can use polynomial regression to fit our data better.
With polynomial regression, we take an optional feature x, and modify it by raising it by to the power of 2 or 3 or any other power. you may also use the square root of your feature x
Some examples of polynomial functions:

a quadratic function

a cubic function
it is usually a good idea to get your features to comparable range of values if you were to perform feature scaling.

Comments