Day 40: Clustering
- Jan 4, 2024
- 3 min read
A clustering algorithm looks at a number of data points and automatically finds data points that are related or similar to each other. In unsupervised learning, you are given a dataset with features (x), but not target labels (y).
Because we don't have target labels (y), we are not able to tell the algorithm what is the right answer (y) that we wanted to predict. Instead, we're going to ask the algorithm to find some interesting structure about this data. Clustering algorithm looks for one particular type of structure in data
K-Means Intuition
The 2 key steps of k-means algorithm are:
Assign every point to the cluster centroid, depending on what cluster centroid it's nearest to
Move each cluster centroid to the average or mean of all the points that were assigned to it
Let's look at an example:
The first thing that the k-means algorithm does is it will take a random guess at where might be the centers of the 2 clusters that you might ask it to find.
In this example, we're going to ask it to find 2 clusters.
The red and blue cross shown is a random initial guess, they are not particularly good guesses, but it's a start.
After making the initial guess for the location of the cluster centroids (center of the cluster), it will go through all of the examples (orange/yellow dots), and for each of them, it will check if it's closer to the red cross or blue cross
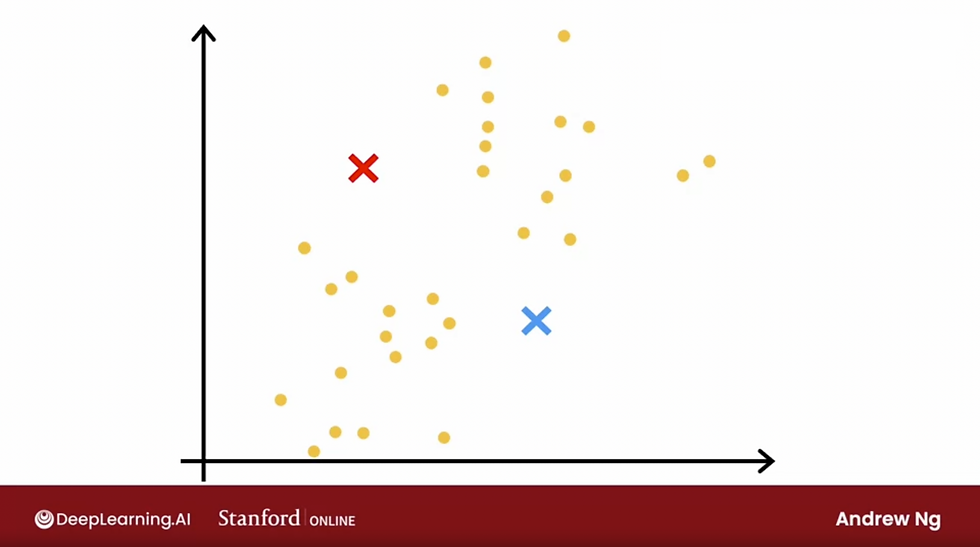
It will then assign each of these points to whichever of the cluster centroids it's closer to.
It will then take the mean of all these red points and move the red cross to whatever the average or mean location of the red dots, it will do the same to the blue.
Now, we have a new location for the red cross and the blue cross.
It will look through all the 30 examples again, and see if it's closer to the new red or blue cross location, and then re-assign them to the new red or blue cross cluster, after going through all 30, it will average/mean again and repeat this process over and over until there are no more changes to the colors of the points or to the locations of the cluster centroids.
At this point, that means k-means clustering algorithm has converged, because applying these 2 steps over and over results in no further changes to either assignment to point to the centroids/location of the cluster centroids.
K-means algorithm
The first step is to randomly initialize k cluster centroids: Mu1, Mu2, ..., Muk
Remember, in our example, we have set k=2, the red cross would be the location of Mu1, and blue cross=Mu2
FYI, Mu1 and Mu2 are vectors, which have the same dimension of your training examples
Repeat {
# assign points to cluster centroids
for i = m:
c[i] := index (from 1 to k) of cluster centroid closest to x[i]When you implement this algorithm, you may find that it's actually a little bit more convenient to minimize the square distance because the cluster centroid with the smallest square distance should be the same as the cluster centroid with the smallest distance
The next step is to move cluster centroids (after all the points have been assigned to its respective cluster):
# move cluster centroids
for k=1 to K:
Muk := average of points assigned to cluster k
}Let's say we have 4 training examples in cluster Mu1 (red cross), we would calculate the new Mu1 location like this: (x1 + x5 + x6 + x10)/4
There is one corner case of this algorithm , which is what happens if a cluster has zero training examples assigned to it? In that case, during the second step, Muk, would be trying to computer the average of zero points and that's not well defined. If that ever happens, the most common thing to do is to eliminate that cluster, and you will end up with (k - 1) clsuers, or if you really need k-clusters, an alternative would be to randomly re-initialize that cluster centroid and hope that it gets assigned at least some point next time around, but it's more common when running k-means to eliminate a cluster if no points are assigned to it.


Comments