Day 11: Introduction to Classification

Classification with logistic regression

Today, we will learn about classification, where your output variable y can take on only one of a small handful of possible values instead of any number in an infinite range of numbers.

We will be using a new algorithm called logistic regression for classification as linear regression would not be suitable. Some examples of classification:

Questions	Answer (y)
is this email spam?	yes or no
is the transaction fraudulent?	yes or no
is the tumor malignant?	yes or no

y can only be one of two values, this is also known as binary classification

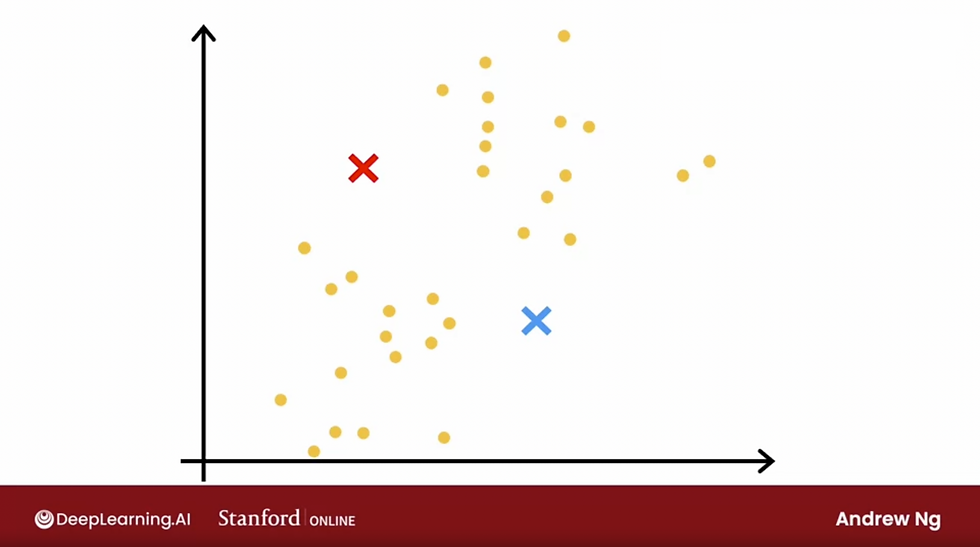
Classification datasets often use symbols to indicate the outcome of an example. Let's take a look:

x_train = np.array([0. , 1, 2, 3, 4, 5])
y_train = np.array([0, 0, 0, 1, 1, 1])

In the example above, positive results are shown as a red-cross with y = 1, negative results are blue-circles with y = 0. this corresponds with the data we entered when x = 5, y = 1.

Sigmoid (Logistic) Function

Let's start by taking a look at a logistic regression plot:

In the example above, we can see in the plot of tumor size on the horizontal axis, and the y labels on the vertical axis.

red-cross indicates malignant tumor (y = 1), and blue-circles indicate benign tumor (x = 0), with blue and red painted areas on the plot to indicate when it's considered benign and when it's considered malignant, the area is separated by the g(z) (sigmoid) function, and its output value is between 0 to 1.

for example, if a patient comes in with a tumor of a certain size, then the algorithm will output a threshold number, suggesting that it's closer or more likely to be malignant or benign

To build out the logistic regression algorithm, there's a mathematical function called the sigmoid function:

e here is a mathematical constant that takes on a value of about 2.7. For example, if z = 100, that would be 2.7⁻¹⁰⁰, which would be a very tiny number.

When z is large, g(z) is going to be very close to 1, conversely, when z is a large negative number (say, -100), g(z) will be very close to 0.

That's why the sigmoid function has this shape where it starts very close to 0 and slowly builds up or grows to the value of 1.

Let's use this to build our logistic regression algorithm:

• calculate z using the same formula, the same one as our linear regression function:

• take that value of z and pass it to our sigmoid function:

• the output will be between 0 - 1

So, our logistic regression function can be written as:

Interpreting the logistic regression output:

• the way to think of the logistic regression output is the probability that the class (label y) will be equal to 1 given a certain input x.

Let's code that in python:

import numpy as np

def sigmoid(z):
	g = 1 / (1 + np.exp(-z))
	return g

NumPy has a function called 'exp()', which offers a convenient way to calculate the exponential e_z of all elements in the input array (z)

extras: how to read a certain mathematical post

probability that y is 1, given input x, parameters w, b