Day 28: Neural Network with softmax output

In order to build a neural network that can carry out multi-class classification, we are going to take the softmax regression model and put it into the output layer of a neural network.

What's going on inside the softmax layer? take a look at the computation below with 10 units and softmax activation.

Improved implementation of softmax

Let's look at 2 computations:

x1 = 2/10_000 # 10_000 is ten-thousand, the underscore was placed for readability

x2 = (1 + (1/10_000) - (1 - (1/10_000) = 2/10_000

When computed on Python:

• x1 would result in 0.000200000

• x2 would result in 0.000199978

You can see that even though they should result in the same result, they're not exactly quite right. There's a way for us to implement softmax function to be more accurate. Let's first take a look at a more numerically accurate implementation of logistic loss:

logistic regression:

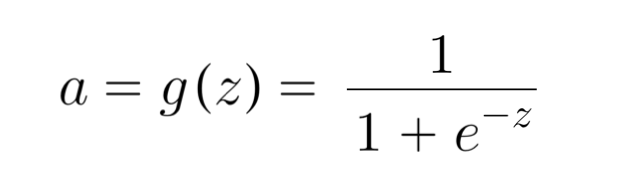
original loss:

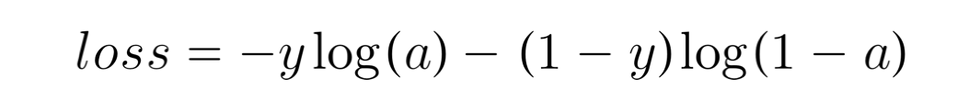
more accurate loss (in code):

In code, you would specify it as linear instead of sigmoid, and add the logit, see below:

Dense(units = 1, activation='sigmoid')

model.compile(loss=BinaryCrossEntropy())

or

Dense(units = 1, activation='linear'

model.compile(loss=BinaryCrossEntropy(from_logits=True))

Note: logits refers to the raw outputs of a model before they're transformed into probabilities. Recall that 'linear' activation is also no activation.

If you take a in the original loss function and expand it to the actual function (1/(1+e^-z)) TensorFlow can rearrange terms in the expression and come up with a more numerically accurate way to compute the loss function. That's what from_logits=True argument causes TensorFlow to do.

The logits is the z, Tensorflow will compute z as an intermediate value, but it can rearrange terms to be computed more accurately. Either of these implementations would be okay, but the numerical roundoff errors can get worse when it comes to softmax.

Classification with multiple outputs

You have learned about multi-class classification, where the output label y can be one of 2 or more potentially many more than 2 possible categories. There's a different type of classification problem called a multi-label classification problem, where each image could contain multiple labels. (as opposed to multi-class where each image could only have one possible label out of N labels).

For example, if you're building a self-driving car, given a picture of what's in front of you, you may have questions such as, is there a car or at least a car? is there a bus? a pedestrian?

One way to do this is to train 2 separate neural network to detect: one for cars, one for pedestrians, and one for buses.

Alternatively, you can train one neural network with 3 outputs and use a sigmoid function for the outputs.