Day 30: Advice for applying Machine Learning
- Oct 13, 2023
- 3 min read
The efficiency of how quickly you can get a ML system to work well will depend on a large part on how well you can repeatedly make good decisions about what to do.
Let's take a look at some advice on how to build ML systems:
let's say you have implemented a regularized linear regression on housing prices, but it makes unacceptably large errors in predictions. What do you try next?
Some examples on what to try:
get more training examples
try smaller set of features
try getting additional features
try adding polynomial features
try decreasing regularization
try increasing regularization
In this section, and the next few sections, we will learn about how to carry out a set of diagnostic.
Diagnostic: a test that you run to gain insight into what is or isn't working with a learning algorithm, to gain guidance into improving its performance
Diagnostics can take time to implement but doing so can be a very good use of your time
Evaluating a model
Once you have trained an ML model. How do you evaluate the model's performance?
Having a systematic way to evaluate performance will provide a clearer path for how to improve the performance of your model.
One technique to try to evaluate your model:
If you have a training set, let's say 10 examples, rather than taking all your data to train the parameters, you can instead split the training set into two subsets
Split the set into two sets: training examples = 7, test examples = 3
What we're going to do here is train the models and parameters on the training set (70%) and then we will test its performance on the test set (30%)
Compute both the test and training error and compare both the train and test performance

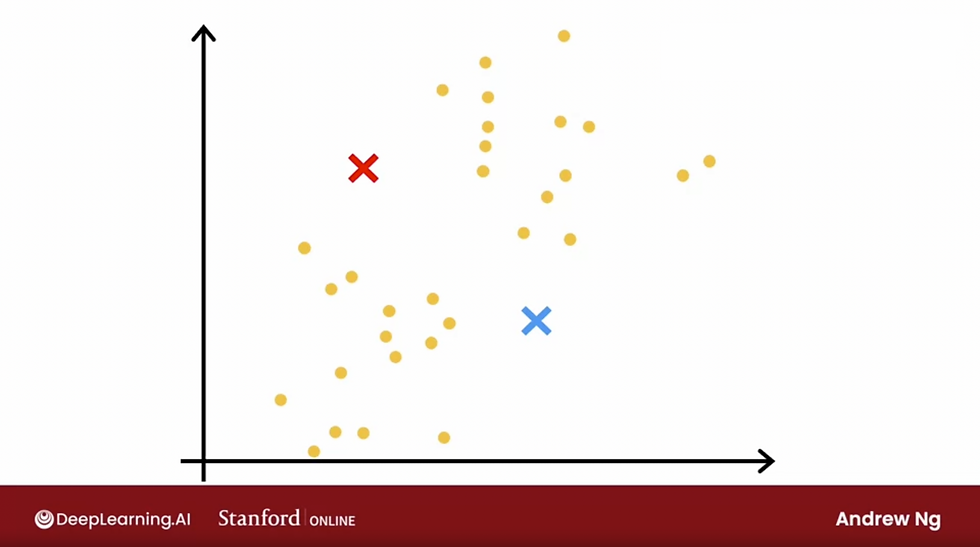
Take a look at the graph in the image above, the red x is the training set, the blue line is the prediction line of the model and it fits the training set extremely well, Jtrain will be low because the average error on your training examples will be zero or very close to zero
In contrast to the test set (the dataset not seen by the model, the 30% that we split earlier, or the purple x), J test will be high because there's a large gap between what the algorithm is predicting, as the estimate of housing price and the actual value of those housing prices
As we can see from the graph above, even though it does great on the training set, it's actually not good at generalizing new examples to new data points that were not in the training set.
Train/Test procedure for classification problem
We have looked at a simple way to evaluate a model's performance on a regression problem, let's take a look at how we can evaluate a model on classification problem:
Measure a fraction of the test set and the fraction of the training set that the algorithm has misclassified
let's say we have set a threshold of 0.5, so if prediction was more than or equal to 0.5 we'll count set y-hat(prediction) as 1, otherwise 0.
Count y-hat != y (prediction label not equal to ground truth (actual) label)
J test would be the fraction of the test set that has been misclassified
J train would be the fraction of the train set that has been misclassified
For a model to be considered performing well, we want to minimize both J-test and J-train, in our regression evaluation above, we can see that Jtrain is fitting the training data very well (Jtrain is low), and Jtest is high (the model is not fitting well at all to data it hasn't seen, in this case, the test set).
We usually consider this a high variance/overfitting problem, that means the model is fitting too well to our training set but fail to generalize or correctly predict on data it hasn't seen.
In the next few articles, we'll go deeper on how we can identify these issues and what we can do to address these problems.

Comments